CSE 247: Shortest Path

Module 6: Shortest Path

Extensions

Extension 1: ( points):

Page not found | Kyle J. Harms

Kyle J. Harms

Menu
Skip to content
Home
Teaching
CSE 247 – Data Structures and Algorithms
CSE 556A – Human Computer Interaction Methods
CSE 556A – Calendar
CSE 556A – Reading Submission
CSE 556A – Project
CSE 556A – Team Member Evaluations
CSE 556A – Syllabus
Research
Puzzle Looking Glass
Publications
About Me

This is somewhat embarrassing, isn’t it?

It seems we can’t find what you’re looking for. Perhaps searching can help.

Search for:

Prim's Minimum Spanning Tree Algorithm
Author: Yonatan David and Tim Heyer

Abstract: We have seen Dijkstra's shortest path algorithm earlier in this course. Prim's Algorithm is similar to Dijkstra's and is used to find the minimum spanning tree of a graph.

In this assignment, you will apply Prim's algorithm and the concept of a minimum spanning tree to a real-world network optimization problem.

Note: Prim's Algorithm is discussed in detail in Section 23.2 (pg. 634) of the text.

Introduction

A spanning tree is a tree derived from an edge-weight graph that touches each vertex of the graph exactly once. The fundamental property of a minimum spanning tree (MST) is that the sum of the weights of its edges is no larger than the weight of any other spanning tree.

As such, the tree will contain all vertices of its corresponding graph, and must visit each vertex in a specific order. The minimum spanning tree of a graph is one that is:

connected
acyclic
inclusive of all vertices
the minimum total weighting for its edges

Useful Applications

Minimum spanning trees have a variety of real-world applications. For example, we use minimum spanning trees to model:

Prim's Algorithm

Instead of trying to find the shortest path from one point to another like Dijkstra's algorithm, Prim's algorithm calculates the minimum spanning tree of the graph. We start at one vertex and select an edge with the smallest value of all the currently reachable edge weights. Algorithms that operate like this—in that they always make the locally optimal choice—are known as greedy algorithms. Your task is to compute the minimum distance, as well as a mapping of the path taken, to visit all vertices using Prim's algorithm as described below.

Given a start vertex, compare the weights of all reachable edges and choose the one with the least weight. If there are multiple edges with the same weight, choose one of the edges.
Visit the vertex to which the edge connects.
Reevaluate all available edges, including previously visited vertices and their respective edges. Choose the edge with the least weight that leads to an unvisited vertex.
Repeat step 3 until all vertices have been visited.

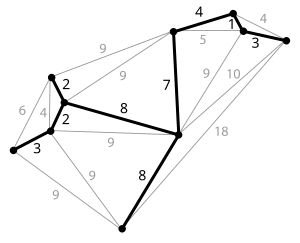
As you visit new vertices, be sure to map the new vertex to the edge you took to reach it in the toEdge map. This map will be used to calculate the total distance traveled and will become your minimum spanning tree.

Problem

For this assignment, you are an engineer working for a telecommunications firm. Your firm wants to introduce landline telephone service to a developing country and has commissioned you for the task. A surveyor has prepared a layout of the cities (vertices) to which you must run telephone lines, as well as the available paths between each city (edges). Due to geographic restrictions, some cities will have multiple paths to reach them and others may have only one. Additionally, each of these paths has a different weight which is the cost of using a given path based on distance, geographic obstacles, and accessibility. You are required to run a telephone line that connects each city in the country (graph) and to do so as efficiently as possible. In other words, minimize the total amount of telephone line used.

Note that telephone service can travel to any city connected to the network you install. As such, every city does not need a wire to every other city; there only needs to be one common wire which connects every city.

With the layout of the country in hand, you must now figure out how to connect every city while minimizing your firm's costs and therefore maximizing their profits. You quickly identify that you'll need to construct a minimum spanning tree of the cities and their distances to determine along which paths you'll need to install wire. Luckily, you're familiar with Prim's algorithm so you fire up Eclipse and begin writing a solution in your favorite programming language, Java.

Your Assignment

Update your repository as usual.
In the prim.util package of the extensions source folder, notice that the graphing classes are similar to those used in the Dijkstra's shortest path lab, but are slightly modified to use an undirected graph instead of the previously used directed graph. Familiarizing yourself with these classes will make this assignment much easier.
In the prim package, find and open the MinimumSpanningTree class.
Complete the run() method using the steps of Prim's algorithm outlined above.
Pass the unit tests (Note: the test can take up to a minute to finish running).

The unit tests work by constructing a graph with a preconfigured minimum spanning tree. While it is true that in general, graphs will often have more than one MST (though all with the same total weight), the graph generated by the unit tests will have only one. Therefore, by following all of the steps in Prim's algorithm you will find and return the same MST known to the test.